Jak stworzyć sieć neuronową
Maciej Mazurek , 8 stycznia 2020

Wstęp
Celem tego artykułu jest przedstawienie koncepcji działania sieci neuronowych, a konkretnie sieci neuronowych typu Feedforward neural network, poprzez skonstruowanie prostego przykładu takiej sieci w języku Python. Do pełnego zrozumienia załączonego do artykułu kodu wymagana jest jedynie umiejętność mnożenia macierzy.
Sieć neuronowa to statystyczny model obliczeniowy stosowany w uczeniu maszynowym. Można o nim myśleć jak o systemie połączonych synapsami neuronów, które przesyłają między sobą impulsy (dane). Sieć neuronowa składa się z trzech warstw: warstwy wejścia (input layer), warstwy ukrytej (hidden layer), oraz warstwy wyjścia (output layer), co ilustruje diagram 1.
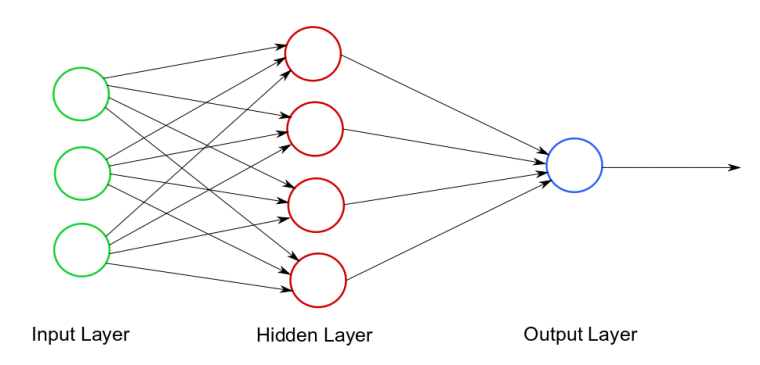
Warstwa wejścia przyjmuje dane wejściowe do obliczeń, w warstwie ukrytej odbywają się wszystkie obliczenia. Wynik tych obliczeń jest przesyłany do warstwy wyjścia.
Na powyższym diagramie okręgi reprezentują neurony, zaś strzałki - synapsy. Każda synapsa ma przypisaną pewną wagę, tzn liczbę, która (nieco upraszczając) określa, jak silnie przesyłana wartość wpływa na ostateczny wynik obliczeń. Żeby przesłać wartość, synapsa najpierw czyta wartość z neuronu wejściowego, następnie wartość tę mnoży przez wagę, by w końcu przesłać wynik do neuronu wyjściowego. Następnie neuron wyjściowy dokonuje obliczeń na dostarczonych mu przez synapsy wartościach i otrzymany wynik przekazuje do wychodzącej z niego synapsy.
Trenowanie sieci neuronowej jest procesem, którego celem jest (nieco upraszczając) dobór odpowiednich wag dla synaps. Zakładamy, że sposób w jaki dokonywane są obliczenia wewnątrz każdego z neuronów jest niezmienny. Trenowanie jest procesem iteracyjnym. Jedna iteracja składa się z dwóch (wykonywanych w podanej kolejności) kroków: propagacji oraz propagacji wstecznej.
Mówiąc w skrócie - propagacja polega na wykonaniu obliczeń na danych wejściowych stosując wagi przypisane synapsom. Propagacja wsteczna mierzy błąd, jakim jest obarczony rezultat propagacji (przez porównanie go z oczekiwanymi wynikami obliczeń, czyli z danymi treningowymi). W zależności od zmierzonego błędu modyfikowane są wagi synaps (można powiedzieć, że dostosowując wagi sieć "uczy się na swoich błędach").
Przykład
W tej sekcji zostanie zaprezentowane, jak skonstruować prostą sieć neuronową implementującą opisane we wstępie koncepcje.
Rozważmy następujący problem. Dla danej trzybitowej dodatniej liczby binarnej (bez znaku) rozstrzygnąć, czy jest ona parzysta. Poniżej przedstawiamy kilka przykładowych danych wejściowych wraz z oczekiwanymi wartościami na wyjściu.
| Dane wejściowe | Oczekiwany wynik |
| 101 | 0 |
| 110 | 1 |
| 010 | 1 |
Powyższa tabelka to (bardzo skromne) zestawienie danych treningowych. Każdej podanej wartości wejścia przyporządkowany jest oczekiwany rezultat obliczeń.
Struktura sieci neuronowej
Na diagramie 2. przedstawiono strukturę naszej sieci neuronowej. Warstwę wejścia tworzą trzy neurony (każdy neuron odpowiada wartości jednego bitu z zapisu binarnego liczby z wejścia). Warstwa ukryta składa się z dwóch neuronów: U1 oraz U2. Neuron U1 sumuje wszystkie liczby, jakie zostały mu przesłane (z odpowiednimi wagami) przez wchodzące w niego synapsy, a następnie tę sumę przekazuje do neuronu U2. Waga synapsy biegnącej od neuronu U1 do neuronu U2 wynosi 1 (jeśli waga jest nieokreślona, domyślna jej wartość wynosi 1). Następnie neuron U2 nakłada na rezultat obliczeń wykonanych w neuronie U1 funkcję aktywacyjną (która zostanie opisana szczegółowo w dalszej części artykułu) i przekazuje wynik (znów z wagą 1) do warstwy wyjścia.
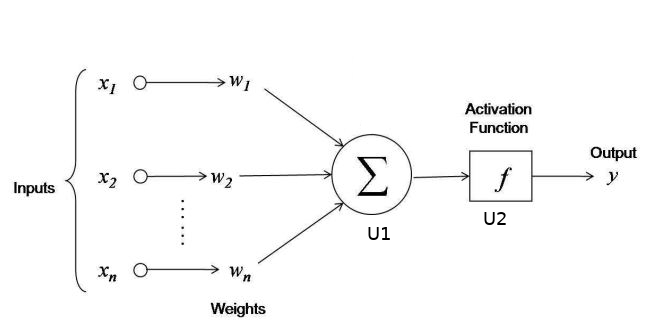
Propagacja
Z tego, co zostało powiedziane powyżej, jasne jest, że wagi muszą mieć z góry ustaloną wartość w momencie, gdy po raz pierwszy wykonywana jest propagacja. Każdą z nich zainicjujemy losowo wybraną liczbą z przedziału (-1, 1), z jednym tylko ograniczeniem. Wartość oczekiwana wag (z pewnych powodów teoretycznych, które tu pomijamy) musi wynosić 0.
Propagacja wykonuje się następująco. Najpierw neurony z warstwy wejściowej są inicjalizowane bitami wejściowej liczby. Następnie wartość każdego neuronu z warstwy wejściowej mnożona jest przez odpowiednią wagę i jest przesyłana do neuronu U1. Neuron U1 sumuje wszystkie trzy wartości.
Rezultat wyliczony w neuronie U1 należy jeszcze "zinterpretować". O tej wartości można myśleć, jako o pewnej mierze (dla wtajemniczonych - prawdopodobieństwie) rozrzutu. Przykładowo, jeśli w neuronie U1 dostaniemy liczbę 332482, to nasza sieć neuronowa twierdzi, że z dużym prawdopodobieństwem poprawnym rezultatem dla danych trzech bitów jest 1. Jeśli natomiast neuron U1 wyliczył liczbę -54387, nasza sieć przewiduje, że poprawny wynik to 0. Jeśli natomiast neuron U1 wyliczył wartość 0, nasza sieć neuronowa nie ma bladego pojęcia, jaki wynik jest poprawny.
Interpretacja, o której mowa, odbywa się w neuronie U2 poprzez zastosowanie odpowiedniej funkcji aktywacji. Istnieje wiele różnych modeli, w których stosowane są przeróżne funkcje aktywacji. Dla naszych celów najlepsza jest funkcja sigmoidalna, której wykres przedstawiamy na rysunku poniżej.
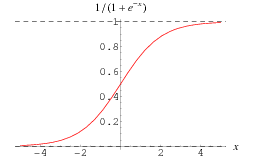
Widać, że ta funkcja "interpretuje" wynik obliczeń z neuronu U1 zgodnie z oczekiwaniami. Im argument jest większy, tym wynik jest bliższy jedynce, im argument jest mniejszy, tym liczba jest bliższa zeru. Zauważmy, że dla argumentu 0 funkcja przyjmuje wartość 0.5.
Propagacja wsteczna
Załóżmy, że wykonujemy jedną iterację procesu trenowania dla pary (110, 1) - pierwsza współrzędna w krotce to dane wejściowe, druga to oczekiwany rezultat. Oznaczmy przez R wartość wyliczoną w neuronie U2 dla opisanych wyżej danych wejściowych i dla wag, jakie w czasie propagacji były przypisane synapsom wychodzącym z neuronów z warstwy wejścia.
Propagację wsteczną zaczniemy od wyliczenia tego, jak bardzo wartość wyliczona podczas propagacji różni się od oczekiwanego wyniku.
Następnie - w zależności od otrzymanego błędu - należy poprawić wagi synaps. W metodzie użytej w tym przykładzie optymalizacja pojedynczej wagi odbywa się następująco.
error = R - expected_result
weight = weight + expected_result * error * d_sigmoid(R)gdzie d_sigmoid(R) jest pochodną funkcji sigmoid w punkcie x=R. Jeśli czytelnika interesuje geneza powyższego wzoru, odsyłamy do opisu regresji logicznej. Orientacyjnie, funkcja mierząca błąd jest funkcją wypukłą, zatem można ją minimalizować schodząc "wzdłuż jej gradientu" - czyli w kierunku jej globalnego minimum.
Kod
import numpy as np
class SimpleNeuralNetwork:
"""
Simple neural network that checks if a given binary representation of a positive number is even
"""
def __init__(self):
np.random.seed(1)
self.weights = 2 * np.random.random((3, 1)) - 1
def sigmoid(self, x):
"""
Sigmmoid function - smooth function that maps any number to a number from 0 to 1
"""
return 1 / (1 + np.exp(-x))
def d_sigmoid(self, x):
"""
Derivative of sigmoid function
"""
return self.sigmoid(x) * (1 - self.sigmoid(x))
def train(self, train_input, train_output, train_iters):
for _ in range(train_iters):
propagation_result = self.propagation(train_input)
self.backward_propagation(
propagation_result, train_input, train_output)
def propagation(self, inputs):
"""
Propagation process
"""
return self.sigmoid(np.dot(inputs.astype(float), self.weights))
def backward_propagation(self, propagation_result, train_input, train_output):
"""
Backward propagation process
"""
error = train_output - propagation_result
self.weights += np.dot(
train_input.T, error * self.d_sigmoid(propagation_result)
)Wyjaśnienie
Na koniec wyjaśnimy, jak przedstawiona powyżej klasa napisana w języku Python realizuje opisaną koncepcję (zakładamy, że czytelnik zna podstawy Pythona).
W konstruktorze klasy SimpleNeuralNetwork najpierw inicjalizujemy generator liczb losowych (linia 10), a następnie określamy początkowe wartości wag liczbami losowymi (linia 11). Początkowe wagi są zapisane jako współrzędne wektora kolumnowego. Po szczegóły odsyłamy do dokumentacji pakietu numpy.
Funkcja proparation jest odpowiedzialna za wykonanie procesu propagacji. Dane wejściowe (trzy bity liczby binarnej) są przekazywane do tej funkcji w postaci wektora o trzech współrzędnych. Polecenie
np.dot(inputs.astype(float), self.weights)liczy iloczyn skalarny wektora wag oraz wektora danych wejściowych, zatem jest to wartość, którą liczy neuron U1. Przekazując tę wartość do funkcji sigmoid otrzymujemy rezultat obliczeń z neuronu U2.
Funkcja backward_propagation implementuje proces propagacji wstecznej. Na początku obliczany jest błąd względem oczekiwanego rezultatu (linia 41). Następnie modyfikowane są wagi synaps. Instrukcja
self.weights += np.dot(
train_input.T, error * self.d_sigmoid(propagation_result)
)wykonuje opisane wcześniej obliczenia na każdej współrzędnej wektora wag. Funkcja np.dot odpowiada za mnożenie macierzy. Wyrażenie train_input.T to po prostu operacja transpozycji wektora (macierzy) train_input.
Krótki program testowy
Poniżej zamieszczono krótki program testowy, który pokazuje możliwości klasy SimpleNeuralNetwork w akcji.
network = SimpleNeuralNetwork()
print(network.weights)
train_inputs = np.array(
[[1, 1, 0], [1, 1, 1], [1, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], ]
)
train_outputs = np.array([[1, 0, 1, 1, 0, 1]]).T
train_iterations = 50000
network.train(train_inputs, train_outputs, train_iterations)
print(network.weights)
print("Testing the data")
test_data = np.array([[1, 1, 1], [1, 0, 0], [0, 1, 1], [0, 1, 0], ])
for data in test_data:
print(f"Result for {data} is:")
print(network.propagation(data))Powyższy kod może dać różne rezultaty (sieć za każdym razem może inaczej sie wyuczyć), ale zawsze są zbliżone do poniższych.
Wyuczone współczynniki dla poszczególnych bitów:
[[ 7.81178357]
[ 7.81137782]
[-23.96202269]]Najwyższą wartość (bezwzględną) przyjmuje ostatni bit i ma wartość ujemną. Co znaczy ze sieć wykryła zależność że wynik zależy praktycznie tylko od negacji ostatniego bitu.
Rezultaty zwracane przez sieć dla 4 prób:
Result for [1 1 1] is:
[0.00023899]
Result for [1 0 0] is:
[0.99959523]
Result for [0 1 1] is:
[9.67974713e-08]
Result for [0 1 0] is:
[0.99959506]Jeśli chcesz poznać inne zastosowania języka Python, zapraszamy do artykułu, który szerzej omawia to zagadnienie.



